Recent work in econometrics and statistical decision theory.
Robust Bayes Treatment Choice with Partial Identification
Revise & Resubmit Sent
With José Luis Montiel Olea, Jörg Stoye, Chen Qiu, and Serdil Tinda
•Econometric Theory
We study a class of binary treatment choice problems with partial identification through the lens of robust (multiple prior) Bayesian analysis. We use a convenient set of prior distributions to derive ex-ante and ex-post robust Bayes decision rules, both for decision makers who can randomize and for decision makers who cannot.
Our main messages are as follows: First, ex-ante and ex-post robust Bayes decision rules do not agree in general, whether or not randomized rules are allowed. Second, randomized treatment assignment for some data realizations can be optimal in both ex-ante and, perhaps more surprisingly, ex-post problems. Therefore, it is usually with loss of generality to exclude randomized rules from consideration, even when regret is evaluated ex post.
We apply our results to a stylized problem where a policy maker uses experimental data to choose whether to implement a new policy in a population of interest, but is concerned about the external validity of the experiment at hand (Stoye, 2012); and to the aggregation of data generated by multiple randomized control trials in different sites to make a policy choice in a population for which no experimental data are available (Manski, 2020; Ishihara and Kitagawa, 2021).
Epsilon-Minimax Solutions of Statistical Decision Problems via the Hedge Algorithm
Under Review
With José Blanchet, José Luis Montiel Olea, Jörg Stoye, Chen Qiu, and Lezhi Tan
A decision rule is epsilon-minimax if it is minimax up to an additive factor epsilon. We present an algorithm for provably obtaining epsilon-minimax solutions for a class of statistical decision problems. In particular, we are interested in problems where the statistician chooses randomly among I decision rules. The minimax solution of these problems admits a convex programming representation over the (I-1)-simplex. Our suggested algorithm is a well-known mirror subgradient descent routine, designed to approximately solve the convex optimization problem that defines the minimax decision rule. This iterative routine is known in the computer science literature as the hedge algorithm and is used in algorithmic game theory as a practical tool to find approximate solutions of two-person zero-sum games. We apply the suggested algorithm to different minimax problems in the econometrics literature. An empirical application to the problem of optimally selecting sites to maximize the external validity of an experimental policy evaluation illustrates the usefulness of the suggested procedure.
Approximate Least-Favorable Distributions and Nearly Optimal Tests via Stochastic Mirror Descent
Under Review
With Lezhi Tan, José Luis Montiel Olea, Chen Qiu, and José Blanchet
We consider a class of hypothesis testing problems where the null hypothesis postulates M distributions for the observed data, and there is only one possible distribution under the alternative. We show that one can use a stochastic mirror descent routine for convex optimization to provably obtain - after finitely many iterations - both an approximate least-favorable distribution and a nearly optimal test, in a sense we make precise. Our theoretical results yield concrete recommendations about the algorithm's implementation, including its initial condition, its step size, and the number of iterations. Importantly, our suggested algorithm can be viewed as a slight variation of the algorithm suggested by Elliott, Müller, and Watson (2015), whose theoretical performance guarantees are unknown.
Drafts in preparation. Available upon request unless linked.
Limited Consideration through Salience
In Progress
With Francesca Molinari and Levon Barseghyan
Empirical Bayes and Gaussian Deconvolution Over Varying Variance
In Progress
Working draft
In this paper, we consider the problem of Gaussian deconvolution. Building off the nonparametric pointwise estimation approach in Fan (1991), we instead consider a mean integrated squared error objective criterion and propose a novel Tikhonov-regularized nonparametric estimate for recovering an underlying distribution convolved by Gaussian noise. We extend these results to a case where data comes in subsequent time periods but the variance of the Gaussian noise grows and stabilizes. These results are then applied to an empirical Bayes setting.
Transfer Performance Evaluation Using Bayes Methods
In Progress
Working draft
I study Bayesian approaches to constructing uncertainty quantification for out-of-sample prediction performance,
and compare them to alternative frequentist methods in the recent literature.
From May to July 2023, I was a Research Assistant at Columbia Business School working under Professor Jing Dong. The premise of the project was the increased prevalence of AI diagnostic technologies (such as IDx-DR) has called into question how current diagnostic workflows can be altered in order to improve patient outcomes. This project took the approach of utilizing stochastic modelling and results in queueing theory to provide a proposed solution to the issue. At the end of the program, I summarized my results in a presentation given to a crowd of fellow RAs, PhD students, and faculty. The presentation, written in LaTeX Beamer, is attached below.
Labor Dynamics Institute Work
From January 2022 to January 2023, I was an Undergraduate Researcher at the Labor Dynamics Institute at Cornell University under Professor Lars Vilhuber. In this work, I replicated numerous economics research papers submitted to a variety of American Economics Association Journals (e.g., AEJ, AER, AEP, etc.), making use of version-control softwares such as GitHub, Bitbucket, and Code Ocean. I also made heavy use of Stata, R, Python, and Matlab. Aside from replication of papers, I also contributed to the replication template used by all of the research assistants in the Replication Lab. The GitHub to said template is linked below.
PRIMO Research Lecture
From June to August 2022, I was a PRIMO Research Fellow at the Harvard Business School, paired with Professor Kyle Myers. In that work, I performed preliminary synthetic control regressions on clinical trial data to answer the following question: Does the market overreact to deaths in gene therapy clinical trials? The position culminated in a presentation given to PRIMO fellows, as well as graduate students and faculty of HBS. The presentation, written in LaTeX Beamer, is attached below. The slides show some of the limitations of synthetic control methods.
Other Work
Normal Numbers Notes
I recently compiled a very brief set of notes about normal numbers mainly based on other sources I came across as I learned about normal numbers.
Logistic Map
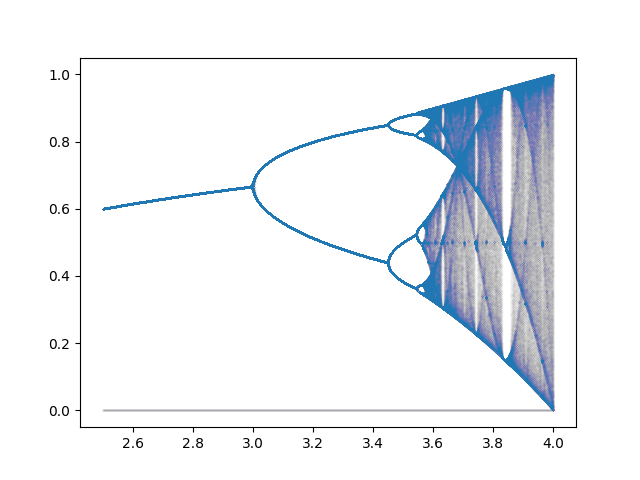
I have coded a Python program to graph the Logistic Map and its chaos and windows. It works by going a certain number of iterations out for initial conditions iterated through an equally spaced set of points between 0 and 1 as the parameter r changes.
Nonstandard Analysis
On December 8th, 2022, I gave a brief lecture on Nonstandard Analysis to undergraduates, graduates, and mathematics faculty. In this lecture, I constructed the hyperreals, discussed the powerful Existential Principle, and briefly motivated possible applications of nonstandard analysis to large economies.
Axiom of Choice Research
Together with James (Ruogu) Zhang, I researched and later gave a lecture to a group of math undergraduates as well as math faculty on the Axiom of Choice. This lecture not only motivated the existence of the Axiom of Choice, but also consisted of elaborate proofs demonstrating the equivalence of the Axiom of Choice to other assumptions, such as Zorn's Lemma, the Well-Ordering Principle, every vector space having a basis, and also a discussion of non-measurable sets, with the Vitali Set being used as a chief example. We also utilized transfinite recursion in some of our equivalence proofs.
Derivation of the Hyperbolic Angle Formula
I have written a short paper that derives the formula for the hyperbolic angle in terms of the coordinates of the unit hyperbola.
